Advanced Encryption Standard
En criptografía, Advanced Encryption Standard (AES), también conocido como Rijndael, es un esquema de cifrado por bloques adoptado como un estándar de cifrado por el gobierno de los Estados Unidos. Se espera que sea usado en el mundo entero y analizado exhaustivamente, como fue el caso de su predecesor, el Data Encryption Standard (DES). El AES fue anunciado por el Instituto Nacional de Estandares y Tecnología (NIST) como FIPS PUB 197 de los Estados Unidos (FIPS 197) el 26 de noviembre de 2001 después de un proceso de estandarización que duró 5 años . Se transformó en un estándar efectivo el 26 de mayo de 2002. Desde 2006, el AES es uno de los algoritmos más populares usados en criptografía simétrica.
El cifrador fue desarrollado por dos criptólogos belgas, Joan Daemen y Vincent Rijmen, ambos estudiantes de la Katholieke Universiteit Leuven, y enviado al proceso de selección AES bajo el nombre "Rijndael", un portmanteau empaquetado de los nombres de los inventores. Rijndael puede ser pronunciado "Raindael",
Desarrollo
Rijndael fue un refinamiento de un diseño anterior de Daemen y Rijmen, Square; Square fue a su vez un desarrollo de Shark.
Al contrario que su predecesor DES, Rijndael es una red de sustitución-permutación, no una red de Feistel. AES es rápido tanto en software como en hardware, es relativamente fácil de implementar, y requiere poca memoria. Como nuevo estándar de cifrado, se está utilizando actualmente a gran escala.
Descripción del cifrado
Estrictamente hablando, AES no es precisamente Rijndael (aunque en la práctica se los llama de manera indistinta) ya que Rijndael permite un mayor rango de tamaño de bloques y longitud de claves; AES tiene un tamaño de bloque fijo de 128 bits y tamaños de llave de 128, 192 ó 256 bits, mientras que Rijndael puede ser especificado por una clave que sea múltiplo de 32 bits, con un mínimo de 128 bits y un máximo de 256 bits.
La clave se expande usando el esquema de claves e Rijndael.
La mayoría de los cálculos del algoritmo AES se hacen en un campo finito determinado.
AES opera en una matriz de 4×4 de bytes, llamada state (algunas versiones de Rijndael con un tamaño de bloque mayor tienen columnas adicionales en el state). Para el cifrado, cada ronda de la aplicación del algoritmo AES (excepto la última) consiste en cuatro pasos:
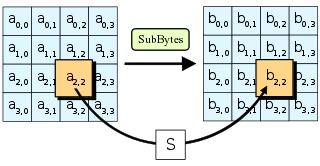
- SubBytes — en este paso se realiza una sustitución no lineal donde cada byte es reemplazado con otro de acuerdo a una tabla de búsqueda.
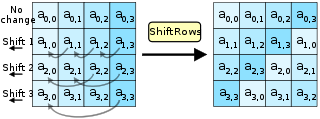
- ShiftRows — en este paso se realiza un transposición donde cada fila del state es rotado de manera cíclica un número determinado de veces.
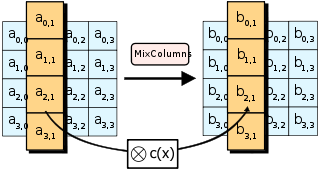
- MixColumns — operación de mezclado que opera en las columnas del «state», combinando los cuatro bytes en cada columna usando una transformación lineal.
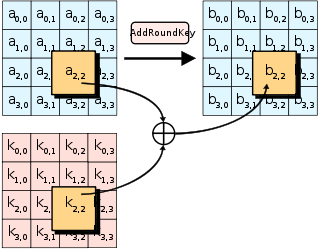
- AddRoundKey — cada byte del «state» es combinado con la clave «round»; cada clave «round» se deriva de la clave de cifrado usando una iteración de la clave.
La ronda final reemplaza la fase MixColumns por otra instancia de AddRoundKey
Etapa SubBytes- Substitución de bits
En la etapa SubBytes, cada byte en la matriz es actualizado usando la caja-S de Rijndael de 8 bits. Esta operación provee la no linealidad en el cifrado. La caja-S utilizada proviene de la función inversa alrededor del GF(28), conocido por tener grandes propiedades de no linealidad. Para evitar ataques basados en simples propiedades algebraicas, la caja-S se construye por la combinación de la función inversa con una transformación afín inversible. La caja-S también se elige para evitar puntos estables (y es por lo tanto un derangement), y también cualesquiera puntos estables opuestos.
La caja-S es descrita en mayor profundidad en el artículo caja-S de Rijndael.
Etapa ShiftRows-Desplazar filas
El paso ShiftRows opera en las filas del state; rota de manera cíclica los bytes en cada fila por un determinado offset. En AES, la primera fila queda en la misma posición. Cada byte de la segunda fila es rotado una posición a la izquierda. De manera similar, la tercera y cuarta filas son rotadas por los offsets de dos y tres respectivamente. De esta manera, cada columna del state resultante del paso ShiftRows está compuesta por bytes de cada columna del state inicial. (variantes de Rijndael con mayor tamaño de bloque tienen offsets distintos).
Etapa MixColumns- Mezclar columnas
En el paso MixColumns, los cuatro bytes de cada columna del state se combinan usando una transformación lineal inversible. La función MixColumns toma cuatro bytes como entrada y devuelve cuatro bytes, donde cada byte de entrada influye todas las salidas de cuatro bytes. Junto con ShiftRows, MixColumns implica difusión en el cifrado. Cada columna se trata como un polinomio GF(28) y luego se multiplica el módulo x4 + 1 con un polinomio fijo c(x). El paso MixColumns puede verse como una multiplicación matricial en el campo finito de Rijndael.
Etapa AddRoundKey- Cálculo de las subclaves
En el paso AddRoundKey, la subclave se combina con el state. En cada ronda se obtiene una subclave de la clave principal, usando la iteración de la clave; cada subclave es del mismo tamaño del state. La subclave se agrega combinando cada byte del state con el correspondiente byte de la subclave usando XOR.
Optimización del cifrado
En sistemas de 32 bits o de mayor tamaño de palabra, es posible acelerar la ejecución de este algoritmo mediante la conversión de las transformaciones SubBytes, ShiftRows y MixColumn en tablas. Se tienen cuatro tablas de 256 entradas de 32 bits que utilizan un total de 4 kilobytes (4096 bytes) de memoria, un Kb cada tabla. De esta manera, una ronda del algoritmo consiste en 16 búsquedas en una tabla seguida de 16 operaciones XOR de 32 bits en el paso AddRoundKey. Si el tamaño de 4 kilobytes de la tabla es demasiado grande para una plataforma determinada, la operación de búsqueda en la tabla se puede realizar mediante una sola tabla de 256 entradas de 32 bits mediante el uso de rotaciones circulares.
Seguridad
Hasta 2005, no se ha encontrado ningún ataque exitoso contra el AES. La Agencia de Seguridad Nacional de los Estados Unidos (NSA) revisó todos los finalistas candidatos al AES, incluyendo el Rijndael, y declaró que todos ellos eran suficientemente seguros para su empleo en información no clasificada del gobierno de los Estados Unidos. En junio del 2003, el gobierno de los Estados Unidos anunció que el AES podía ser usado para información clasificada:
- "The design and strength of all key lengths of the AES algorithm (i.e., 128, 192 and 256) are sufficient to protect classified information up to the SECRET level. TOP SECRET information will require use of either the 192 or 256 key lengths. The implementation of AES in products intended to protect national security systems and/or information must be reviewed and certified by NSA prior to their acquisition and use." —
Este hecho marca la primera vez que el público ha tenido acceso a un cifrador aprobado por la NSA para información super secreta (TOP SECRET). Es interesante notar que muchos productos públicos usan llaves de 128 bits por defecto; es posible que la NSA sospeche de una debilidad fundamental en llaves de este tamaño, o simplemente prefieren tener un margen de seguridad para documentos super secretos (que deberían conservar la seguridad durante décadas en el futuro).
El método más común de ataque hacia un cifrador por bloques consiste en intentar varios ataques sobre versiones del cifrador con un número menor de rondas. El AES tiene 10 rondas para llaves de 128 bits, 12 rondas para llaves de 192 bits, y 14 rondas para llaves de 256 bits. Hasta 2005, los mejores ataques conocidos son sobre versiones reducidas a 7 rondas para llaves de 128 bits, 8 rondas para llaves de 192 bits, y 9 rondas para llaves de 256 bits (Ferguson et al, 2000).
Algunos criptógrafos muestran preocupación sobre la seguridad del AES. Ellos sienten que el margen entre el número de rondas especificado en el cifrador y los mejores ataques conocidos es muy pequeño. El riesgo es que se puede encontrar alguna manera de mejorar los ataques y de ser así, el cifrador podría ser roto. En el contexto criptográfico se considera "roto" un algoritmo si existe algún ataque más rápido que una búsqueda exhaustiva - ataque por fuerza bruta. De modo que un ataque contra el AES de llave de 128 bits que requiera 'sólo' 2120 operaciones sería considerado como un ataque que "rompe" el AES aun tomando en cuenta que por ahora sería un ataque irrealizable. Hasta el momento, tales preocupaciones pueden ser ignoradas. El ataque de fuerza bruta más largamente publicitado y conocido ha sido contra una clave de 64 bits RC5 por distributed.net.
Otra preocupación es la estructura matemática de AES. A diferencia de la mayoría de cifradores de bloques, AES tiene una descripción matemática muy ordenada. Esto no ha llevado todavía a ningún ataque, pero algunos investigadores están preocupados que futuros ataques quizá encuentren una manera de explotar esta estructura.
En 2002, un ataque teórico, denominado "ataque XSL", fue anunciado por Nicolas Courtois y Josef Pieprzyk, mostrando una potencial debilidad en el algoritmo AES. Varios expertos criptográficos han encontrado problemas en las matemáticas que hay por debajo del ataque propuesto, sugiriendo que los autores quizá hayan cometido un error en sus estimaciones. Si esta línea de ataque puede ser tomada contra AES, es una cuestión todavía abierta. Hasta el momento, el ataque XSL contra AES parece especulativo; es improbable que nadie pudiera llevar a cabo en la práctica este ataque.
Ataques de canal auxiliar
Los ataques de canal auxiliar no atacan al cifrador por debajo, sino las implementaciones del cifrador en sistemas que pierden datos involuntariamente.
En abril de 2005, D.J. Bernstein anunció a Ataque temporizado de cache que solía romper un servidor a medida que usaba el cifrado AES para OpenSSL. Este servidor fue diseñado para dar la mayor cantidad de información acerca del tiempo como fuera posible, y el ataque requería cerca de 200 millones de ficheros de texto plano. Se dice que el ataque no es práctico en implementaciones del mundo real ; Bruce Schneier llamó a esta investigación un "bonito ataque temporizado".
En octubre de 2005, Adi Shamir y otros dos investigadores presentaron un artículo demostrando varios ataques temporizados de cache contra AES. Uno de los ataques obtuvo una clave de AES entera luego de tan solo 800 escrituras, en 65 milisegundos. Este ataque requiere que el atacante pueda ejecutar programas en el mismo sistema que realiza el cifrado de AES.
No hay comentarios:
Publicar un comentario